何昱琪 李德禹



摘 要:为了降低分解型算法求解大规模问题的运行时间成本,结合分解型多目标进化算法(MOEA/D)和Spark分布式计算框架的特点,提出了一个主从分布式分解型多目标进化算法(MODEA/D-RDD)。在新的方案中每个Map保存且进化一个子问题,从而通过多个Map分布式计算提高效率。测试例上的实验结果表明,在求得解集质量不明显降低的前提下,全局种群进化方案能够有效缩短求解多目标问题的计算时间。
关键词: Spark计算框架;多目标优化;MOEA/D算法
中图法分类号: TP391 文献标识码:A文章编号:2096-4706(2021)22-0066-05
Abstract: In order to reduce the running time cost of decomposition algorithm for solving large-scale problems, a master-slave distributed multi-objective evolutionary algorithm (MODEA/D-RDD) is proposed based on the characteristics of the decomposition multi-objective evolutionary algorithm (MOEA/D) and Spark distributed computing framework. In the new scheme, each Map saves and evolves a sub problem, so as to improve the efficiency through multiple Map distributed computing. The Experimental results on test cases show that the global population evolution scheme can effectively shorten the computational time on solving multi-objective problems on the premise that the quality of the solution set is not significantly reduced.
Keywords: Spark computing framework; multi-objective optimization; MOEA/D algorithm
0 引 言
MOEAs(Multi-objective Evolutionary Algorithm Based on Decomposition, MOEA/D)算法的主要思想是将复杂的MOP进行分解,得到一组标量子问题,在每次进化迭代的过程中,同时对所有子问题进行处理,得到由各个子问题的解构成的帕累托最优解集。研究发现其分解的特性在求解效率上相对指标型和帕累托型的MOEAs有所提高,但是其求解计算密集型MOP的时间成本依然很高[1],因此时间成本的控制也是MOP问题的一个重要研究方向。分布式计算是大数据时代的一个主流趋势,在提升算法的运算效率方面产生了非常大的影响。为了降低求解MOP问题的时间成本,一个值得考虑的方法是将分布式计算的概念引入到多目标进化算法中。
Hadoop、Spark是目前比较流行的分布式计算框架。Hadoop是出现比较早的一个分布式计算框架,其中用来执行分布式计算的计算框架MapReduce非常适合对离线的大批量数据进行处理,但Hadoop并不适用于需要多次迭代的运算,因为其每次迭代都需要进行IO操作,磁盘IO开销比较大。Spark是一种基于内存进行计算的分布式框架,适合于对迭代类型的算法进行分布式计算。为了减少时间成本,许多学者尝试将分布式计算应用于多目标优化算法。2003年Deb提出了分布式岛屿模型MOEAs的分布式计算方案[2]。2008年Daniela Zaharie提出基于MPI的分层结构的分布式MOEAs[3]。2010年,Sadasivam提出基于分布式框架MapReduce 的混合GA-PSO的分布式算法[4]。2018年,Spark 分布式框架 NSGA-Ⅱ的分布式方案被提出[5]。结合分解型MOEAs的特点,选择Spark分布式计算框架对多目标优化算法进行分布式设计是一个可行的研究方案。本文提出了一个主从分布式多目标优化算法全局优化方案。每个Map保存且进化一个完整大小的种群,从而通过多个Map分布式计算提高效率,降低分解型MOEAs求解MOP问题的时间成本。
1 基于Spark平台的MOEA/D 算法模型
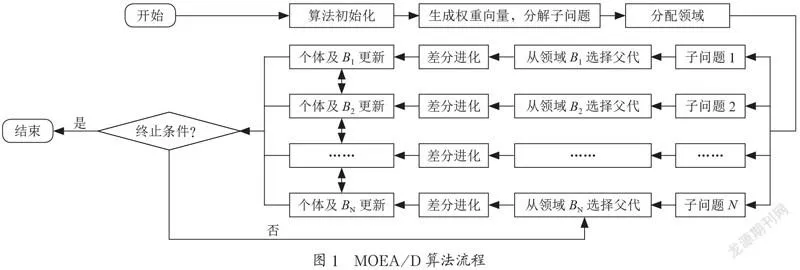
在面对实际问题中的计算密集型优化问题,串行的分解型MOEAs的时间成本依然不够理想。从图1可以看出,分解型多目标进化算法每个子问题都是共同的步骤,就是对子问题的迭代计算,而这一步骤随着问题的复杂程度的提高所需要耗费的计算时间也随之增长,是整个算法中耗时较大的一个部分,并且此部分的处理对算法解集质量的影响也比较小。为了在得到与串行算法质量相当的解集的前提下,降低分解型MOEAs的时间成本,提出一种基于Spark的主从分布式的MOEA/D算法。
1.1 MOEA/D算法
MOEA/D利用分解的思想将复杂的多目标优化问题转变为一系列的单目标问题。每个标量子问题分配一个邻域,利用聚合函数计算每个子问题的聚合函数值,并在领域内通过进化计算产生新的个体,并更新各领域内的差解(不好的个体)。这样,各个子问题之间相互协作同时优化,寻找最优的Pareto解集。MOEA/D算法流程如图1所示。
1.2 基于Spark框架的主从分布式计算框架
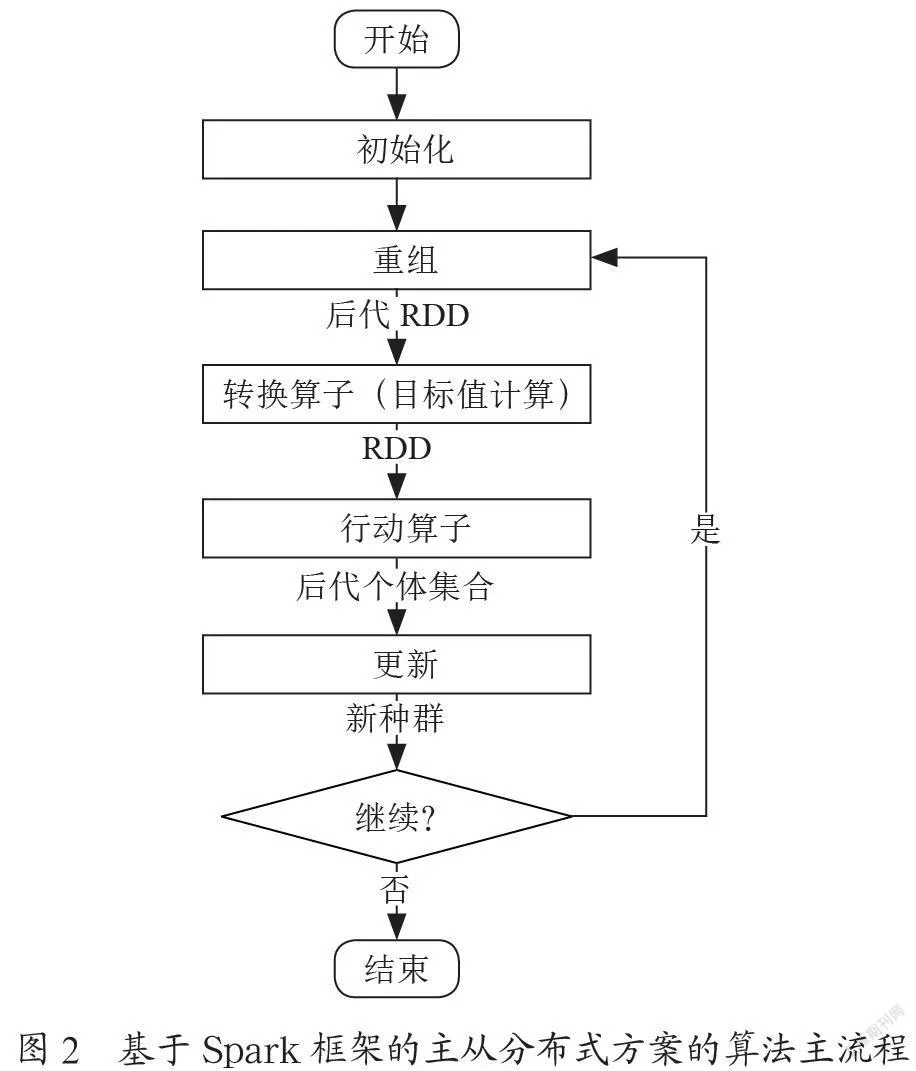
Spark是当前主流的开源分布式计算框架之一,基于内存进行计算的方式使得Spark,相比MapReduce更适合用于需要迭代执行的算法。同时,Spark的一个特殊的数据结构是弹性分布式数据集RDD对分布式内存的抽象使用。Spark的所有分布式操作都是基于RDD的,RDD是Spark最核心的部分,它的特点是可分区,各个分区的操作并行执行。作为一个记录集合,RDD是只读的,可以对RDD执行两种操作算子——转换(Transformation)算子和行动(Action)算子。基于Spark框架的主从式分布计算框架如图2所示。
2 基于Spark框架的分解的多目标优化算法(MOEA/D-RDD)
根据上面设计的Spark算法总流程以及MOEA/D的特点,我们为MOEA/D设计了一中基于子问题并行计算的分布式优化算法MOEA/D-RDD。算法流程为:
算法 2-1:MOEA/D-RDD 算法主框架
1:Initialization
2: pop ← initializePopulation() //初始化种群
3: initializeDirectionVector() //初始化方向向量
4: initializeNeighborhood() //初始化邻居向量
5:while (进化结束条件未到达) do
6: children[] //
7: for i : 0 → N do //分布式计算每个子问题
8: parents:parentSelection() //选择操作
9: child:crossover(parents) //交叉操作
10: child:mutation(child) //变异操作
11: children[i] = child
12: children:distributeEvaluateObj(children) //分布式计算
13: for i:0 → N do
14: child = children[i]
15: updateIdealPoint(child) //更新理想点
16: updateNeighborhood(child) //更新邻居向量
17:获取最终得到的种群 pop 中不被支配的个体,构造帕累托解集 PS
18:根据 F(PS)映射得到帕累托前沿 PF
算法利用Spark 框架将第一部分产生的后代个体集合按照子问题分配到RDD的各个分区中,并对各个分区并行执行转换算子和行动算子。在转换算子中,各个分区并行地对分区中的个体执行目标值计算操作并产生含有目标值的后代个体集合的RDD;对转换算子操作得到的RDD执行行动算子,触发Spark作业并得到所有含有目标值的后代个体构成的集合。迭代计算得到的后代个体集合对原始种群执行更新操作,得到新一代种群。
3 实验结果分析
3.1 测试函数
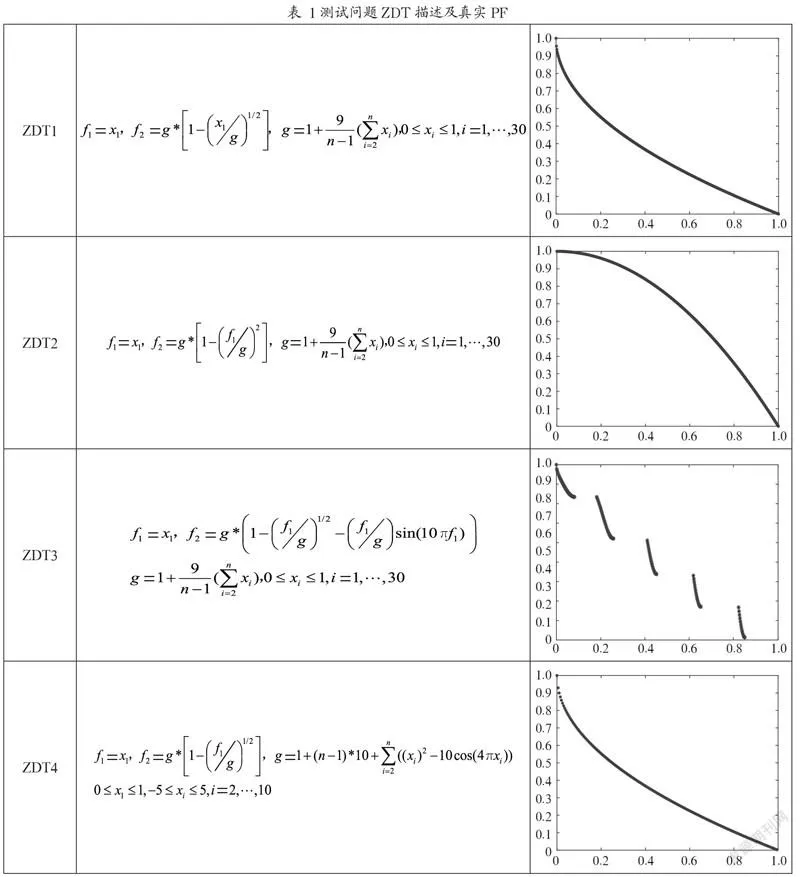
选取了四个测试问题,分别是ZDT1、ZDT2、ZDT3、ZDT4,为了能更直观地展示实验效果、便于在Spark上运行MOEA/D,使用的四个测试问题都为二目标测试问题,这四个测试问题的描述如表1所示。其中,曲线图表示的是真实Pareto前沿,横坐标是二目标问题的Function1的函数值,纵坐标是二目标问题的Function2的函数值。
3.2 实验结果
实验结果均采用的是MOEA/D以本地模式运行以及MOEA/D在Spark集群上运行的结果,主要比较对象是在Spark上的以本地模式运行的串行MOEA/D,既相当于在一台机器上以单线程模式运行的MOEA/D和在基于YARN的Spark集群上以多机器多线程模式运行的 MOEA/D。
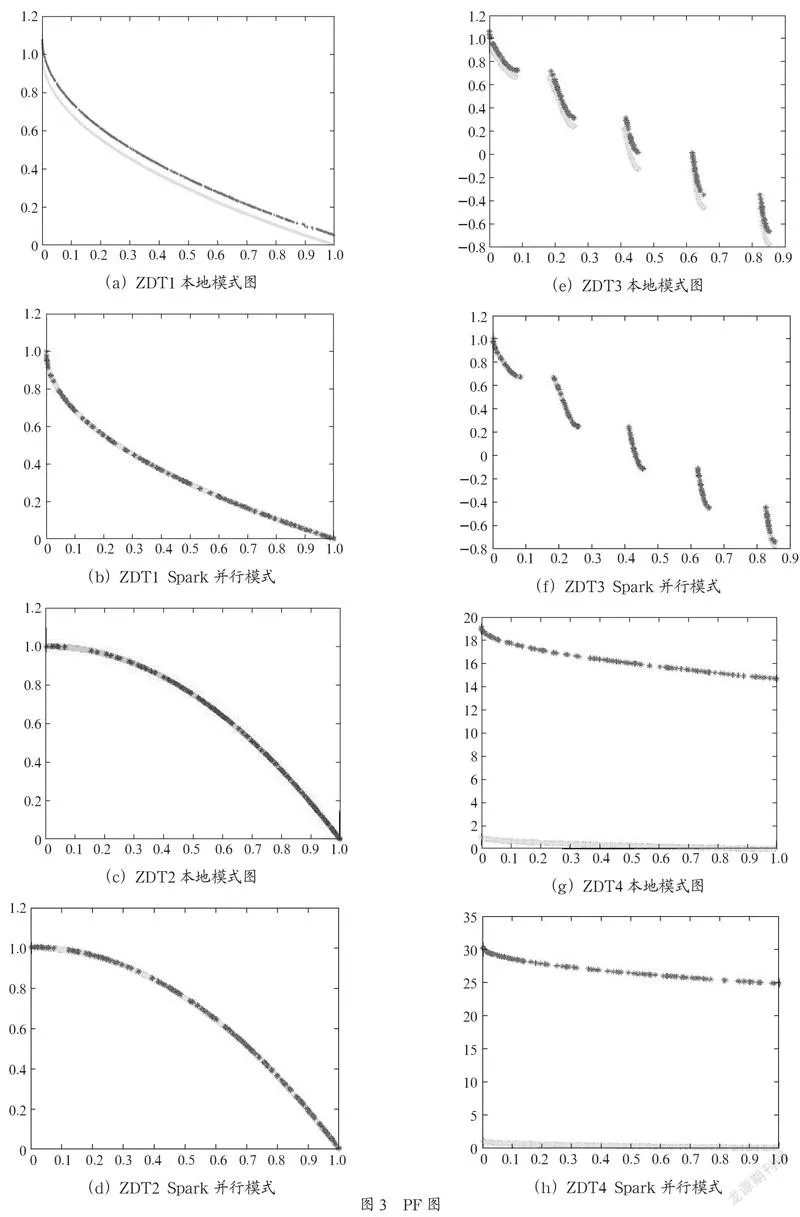
统一多目标问题的种群大小200,邻居大小5,迭代次数100。如图3所示的计算结果散点图横坐标是二目标问题的Function1的函数值,纵坐标是二目标问题的Function2的函数值,散点图中的多个点都是计算得出的最优解。
3.3 结果分析
优化问题除了需要得到较优质的解之外,还有一个运行的效率这个重要的指标。因此,进行分布式优化算法的比较,加速比(Speed-up)是需要考虑的方面之一。
对多目标优化算法和分布式多目标优化算法的加速比统计比较。实验效率分析如表2所示。
评价计算的解与Pareto前沿相近的程度,其中收敛性和多样性为两个主要考虑的方面。在表3实验质量分析表中,Mean代表真实Pareto前沿面上的点集到获取的解集的最小距离的平均值,又因为真实Pareto前沿面是分布均匀的,因此数值越小表明计算得到的解集的收敛性和多样性越好。
实验结果表明,在求得的解集质量没有明显下降的情况下,基于Spark的 MOEA/D 算法取得了非常好的优化效果,大大缩短了求解多目标问题的计算时间。
4 结 论
文中利用基于分解的多目标优化算法MOEA/D的分解特性,通过种群分布式存储和处理的方式,在Spark计算框架上实现了可分布式计算的MOEA/D多目标优化算法。同时也验证了多目标优化算法分布式运行相比非分布式运行的优势。
在以后的研究中,可以探索用本文实现的分布式MOEA/D算法解决具体的多目标优化问题,通过具体的多目标优化问题来对算法的有效性进行更深入的验证。
参考文献:
[1] FONSECA C M, FLEMING P J. An overview of evolutionary algorithms in multiobjective optimization [J].Evolutionary computation, 1995,3(1):1-16.
[2] DEB K,ZOPE P,Jain A. Distributed computing of Pareto-optimal solutions with evolutionary algorithms [C]//Proceedings of the 2nd international conference on Evolutionary multi-criterion optimization.Springer-Verlag:534-549.
[3] ZAHARIE D, PETCU D, PANICA S. A Hierarchical Approach in Distributed Evolutionary Algorithms for Multiobjective Optimization [J].Lecture Notes in Computer Science,2008,4818:516-523.
[4] SADASIVAM G S,SELVARAJ D. A novel parallel hybrid PSO-GA using MapReduce to schedule jobs in Hadoop data grids [C]//2010 Second World Congress on Nature and Biologically Inspired Computing (NaBIC).Kitakyushu:IEEE,2010:377-382.
[5] DONKAL G, VERMA G K. Securing Big Data Ecosystem with NSGA-II and Gradient Boosted Trees Based NIDS Using Spark [C]//2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS).Madurai:IEEE.2018:146-151.
作者简介:何昱琪(2001—),女,汉族,浙江义乌人,本科在读,研究方向:数据处理、数据分析统计。李德禹(2001—),男,汉族,安徽阜阳人,本科在读,研究方向:算法设计与分析、数据处理。
