徐黎明 邓华 刘亮
摘 要:仓储中心的叉车调度和车位分配是解决仓储中心工作效率低下的关键。通过贪婪遗传算法,解决天津L综合仓储中心的车辆的车位分配以及叉车作业优化调度问题。首先获取车辆的偏好车位,在生成初始可行解的过程中,运用贪婪算法将新到仓储中心的车辆分配到最先空闲的车位,减少车辆等待的时间,最后运用遗传算法的选择、交叉和变异操作不断产生适应度较高的解,结合实际问题,最终实现综合仓储中心的运输车辆车位的分配以及叉车作业调度的联合优化。
关键词:贪婪遗传算法;车位分配;叉车调度;偏好车位
Abstract:Forklift scheduling and parking space allocation are the key to solve the low efficiency of storage center. The greedy genetic algorithm is used to solve the problem of vehicle space allocation and forklift operation optimization scheduling in Tianjin L comprehensive storage center. In the process of generating the initial feasible solution,the greedy algorithm is used to allocate the new vehicles to the first idle parking space,so as to reduce the waiting time,finally,the selection,crossover and mutation operations of genetic algorithm are used to produce solutions with high adaptability. Combined with practical problems,the allocation of transportation vehicle parking space in the comprehensive storage center and the joint optimization of forklift operation scheduling are finally realized.
Keywords:greedy genetic algorithm;berth allocation;shore bridge scheduling;preference berth
0 引 言
随着经济的发展,我国的综合仓储中心逐渐增多。但由于仓储中心管理水平的低下,货物积压、货车停滞的现象不断发生,导致仓库的工作效率降低,运输车辆的车位分配和叉车调度优化是解决该问题的核心。彭小利等[1]在智能仓库的环境下,结合RFID技术建立数学和叉车作业分配算法来提高仓库的工作效率;马骊等[2]在不对现有的仓储空间进行扩大的条件下,提出仓储中心的主动式仓储调度算法来降低阻塞时间;杨文强等[3]通过将完工时间最小视为目标,提出一种改进的布谷鸟智能算法来对仓储进行调度;张晓磊[4]通过灰色多层次弱收敛序列系数拟合出最短线路,建立了饲料运输车辆的调度优化方案。上述的研究多是以车辆停靠车位的最小时间为目标进行优化,没有考虑车辆停靠车位时的偏好性以及时间窗的限制。本文建立了带有车辆停靠偏好性的数学模型,并提出相应的算法,得出使得车位分配和叉车联合调度问题最优的分配结果。
1 问题描述
本文基于合作项目对位于天津的L综合仓储中心进行车位分配和叉车作业调度研究,L仓储中心主要用于储存进出口贸易的货物以及生鲜等产品,进出L仓储中心的车辆主要是进行装卸物资。由于L仓储中心的各个仓库的装卸区域有限,所以会造成车辆有一定时间的延迟,本文定义c1来表示单位延迟成本,定义偏移偏好车位的成本为c2,定义每个叉车的单位服务成本为c3。本文综合考虑车辆装卸作业的紧迫程度(通过c1体现)、车位叉车配置数量经济性需求(通过c3体现)、车辆对仓库就近作业距离经济性需求(通过c2体现)。
2 模型描述
2.1 偏好车位的确定
假设有30辆大型货车分别在不同的时间段内到达L仓储中心进行装卸载作业。其中15辆大型货车进行卸货任务,另外15辆大型货车进行装货任务。对于装货的车辆,数据集中显示了待装货物位置的具体仓库区号,因此当这些车所停靠的车位距离这些仓库越近,显然越有利于后续的车辆运输操作。因此在此通过计算这些仓库到各个车位的距离,然后取距离最小的车位作为装货车辆的偏好车位。具体如式(1)所示:
2.2 参数设定
(1)假设单位延迟时间成本c1=5元;
(2)假设单位远离偏好车位的成本c2=100元;
(3)假设每个叉车参与工作的成本c3=100元;
(4)引入变量wi,来表示货车i完成装卸载任务所需的叉车总工时数。
2.3 模型假设
(1)到库车辆都必须且只能停一次,在装卸过程中不考虑转移仓库情况;
(2)每辆车均有一个偏好车位,当车辆停泊在偏好车位时,集卡的运输距离最短;
(3)每辆车都有可分配叉车数的上限和下限,且在车辆装卸过程中作业的叉车数不变;
(4)分配给车辆的叉车在装卸任务开始后直至装卸任务结束不能中途停止;
(5)不考虑多个叉车同时作业时相互干扰对叉车工作效率的影响;
(6)所有车辆都能按照计划时间准时到达仓库,进行停车装载操作。
2.4 模型与符号说明
2.4.1 参数说明
V:计划周期内到仓储中心车辆的数量;
B:仓储中心可用车位数;
M:极大的正数;
Q:总岸桥数;
ai:车辆i的计划到仓储中心时间;
bi:车辆i的计划离散时间;
pi:车辆i的偏好车位;
2.4.2 决策变量
Uijk:若车辆i在j车位按次序k被服务则取值为1,否则为0;
qi:分配给车辆i的叉车数。
2.4.3 从属变量
Ei:车辆i的进入仓储中心时刻;
Di:车辆i的离开仓储中心时刻;
Uit:若车辆i在t时刻被服务则取值为1,否则取值为0。
2.4.4 数学模型
根据上述的定义结合车位分配和叉车调度问题,建立的数学模型具体如式(2)至(15)所示:
式(2)是最小化三大成本:延迟成本+偏离偏好车位成本+叉车服务成本。式(3)和(4)保证任何车辆在各自的时间窗口内都进行装卸载工作。式(5)使得单辆车只停靠仓库的机会有且仅有一次。式(6)规定了单个车位在服务的时候仅能接收一辆车。式(7)规定了车辆进出仓储中心时的服务顺序。式(8)可以避免车辆在同一个车位被服务的时候产生时间冲突问题。式(9)可以保证在任意的一个时刻的叉车的数量不会比仓库中现有的叉车数目要多。式(10)必须满足每辆车所需的叉车台数,即每辆车工作完才能离开。式(11)限制了分配给每个车位的叉车数。式(12)保证了工作时间上的连续,以及在时间窗内必须完成所有工作。式(13)(14)(15)定义了决策变量和从属变量的取值范围。
3 贪婪遗传算法
对于小规模的车位与叉车调度问题,传统的商业软件Lingo、CPLEX软件等能够进行求解。但随着车辆数量的增加,问题的规模呈指数型增长,具有全局寻优能力的遗传算法可以更好地求解这一问题。
3.1 个体编码及种群初始化
本文遵循先到先服务原则为到仓储中心车辆竞争分配车位,因此车辆的安排顺序是确定的。在本次遗传算法的求解过程中,每个种群个体用(4×30)的数组进行,如表1所示。
鉴于模型约束较多,在算法设计中将约束条件嵌入算法结构,从而降低模型求解难度。结合具体问题,在设计染色体编码方面做出如下改进:对于每一个染色体的前面9列,分别在第一行填入1~9的全排列,考虑到1、2、8三辆车具有偏好车位,让它们停靠在各自的偏好车位上,改进后的个体编码如表2所示。
式(17)车辆被严重延迟,车辆实际被服务时间都晚于计划离港时间,因增加叉车数qj已经失效,需要同时增加同一车位处上一辆车的qi和qj来缩短服务时间,使得Ej和Dj都落入时间窗内。在本文中,针对式(16)的情况,主要先通过增加qj来实现,如果qj= 仍无法实现使Ej和Dj都落入时间窗内,在考虑增加同一车位处,上一辆车qi;对于式(17)情况,直接令qj= ,然后通过增加同一车位处上一辆车qi,使得Ej和Dj都落入时间窗内。
3.2 遗传算子
3.2.1 算子的选择
本文在选择算子方面使用的是传统的轮盘赌算法,由于目标是求取极小化问题,因此对每个染色体的所对应的函数值取倒数转化为适应度。适应度越大的个体被挑选到的概率越大。
3.2.2 算子的交叉和变异
通过对模型的具体分析可知将编号为10的车辆安排到某一车位的关键因素在于安排给前九的车辆在各自车位上离泊时间的长短。若第i辆车由于货物量少或安排的叉车数很多,最早离开该车位,那么第10辆车就会安排到该车位,应该叉车数的多少会对后续的结果产生影响。因此交叉操作本文主要对叉车数进行操作,交叉操作如图1所示;在染色体突变方面,由于本问题的染色体较长,因此设计两个突变点进行变异,变异的部分仍然是叉车数,如图2所示。对于变异的点,随机生成一个[,]的随机数,插入到原染色体中,如图2的虚线框所示,这样就完成了染色体的变异操作。
4 算例分析
4.1 算例背景
本文针对天津L综合仓储中心的车位与叉车调度进行研究,该综合仓储中心的日常基本工作流程为:装有货物的车辆到达指定车位,由车位处的叉车卸货物到仓库,然后叉车返回车位或者到下一个仓库区取货。该仓储中心遵循先到先服务原则为车辆竞争分配车位,同一车位在同一时间只能接收一辆车,且车辆采用连续装卸货方式,一旦进入车位立即开始作业,完成装载任务后立即离开车位,不考虑车辆移泊情况。由于该仓库有足够多的叉车,但考虑成本问题,需要制定出一个综合的车辆停泊计划与叉车分配计划。
4.2 运行结果
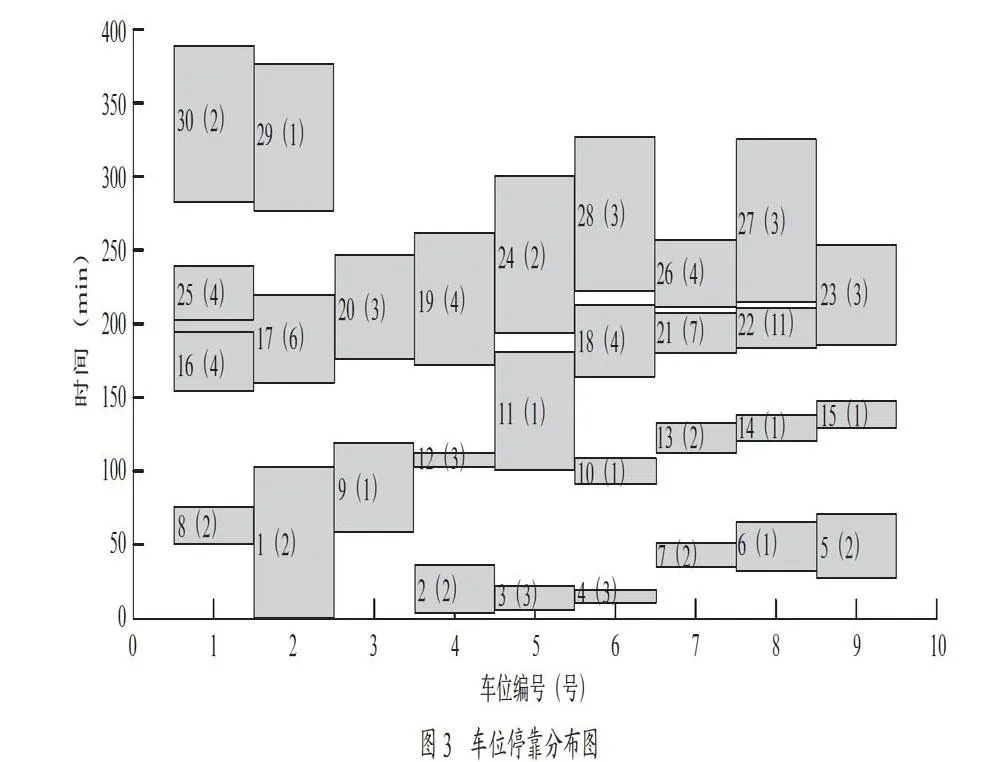
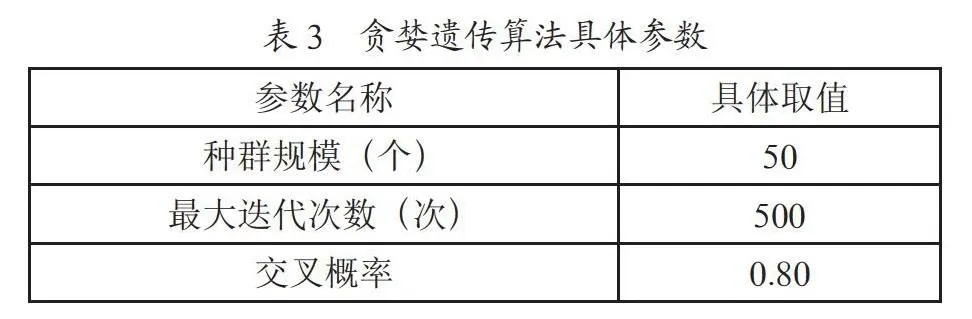
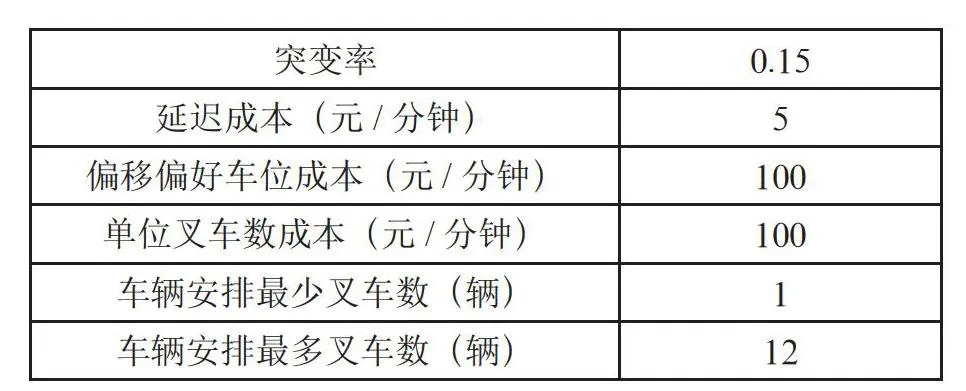
运用MATLAB软件进行编程求解上述问题。贪婪遗传算法的具体参数说明如表3所示。
图3为运行的车位停靠分布图,图钟横轴表示停靠的车位编号,纵轴表示停靠时间,如图中1(2)表示编号为1的车辆停靠在车位2上,安排的叉车个数为2个,其中高度表示在仓储中心的停留的时间。
5 结 论
本文提出了一种时间窗限制条件下的仓库车位与叉车联合调度问题,通过对该问题建立模型,计算获取车辆的偏好车位,生成初始可行解,运用贪婪算法将新到仓储中心的车辆分配到最先空闲的车位,从而减少车辆等待的时间,最后运用传统遗传算法的选择、交叉和变异操作不断产生适应度较高的解,最终实现L综合仓储中心的作业优化调度问题的求解。不足之处在于本文未考虑仓库牵引车作业的时间等因素,下一步的研究可以和牵引车作业结合,对车辆装卸货所用到的所有资源进行整合优化。
参考文献:
[1] 彭小利,廖婷.制造物联环境下智能仓库叉车作业分配算法研究 [J].电子设计工程,2018,26(14):6-9.
[2] 马骊,王银珠,张敏,等.大型物流配送中心的主动式仓储调度策略及其性能分析 [J].西安财经学院学报,2018,31(1):63-68.
[3] 杨文强,郭昊,李勇峰.布谷鸟算法求解组装车间仓储调度优化问题 [J].电子测量与仪器学报,2016,30(10):1506-1511.
[4] 张晓磊.依赖灰色多层次弱收敛序列系数的农村饲料物流车辆调度优化 [J].物流科技,2020,43(1):6-8+25.
作者简介:徐黎明(1993—),男,汉族,安徽太和人,硕士,研究方向:复杂系统仿真与优化;邓华(1977—),男,汉族,四川绵阳人,系主任,副教授,博士,研究方向:质量工程、运营与供应链管理;刘亮(1979—),男,汉族,山东德州人,副教授,博士,研究方向:复杂系统仿真与优化、工业工程与精益管理创新。
